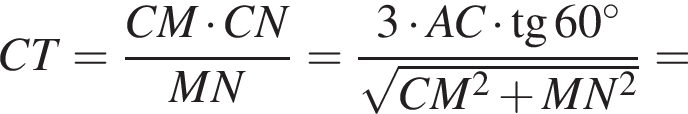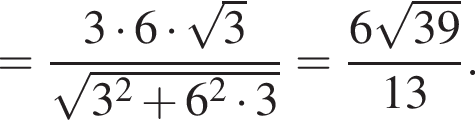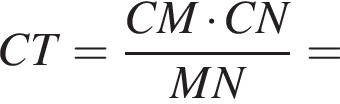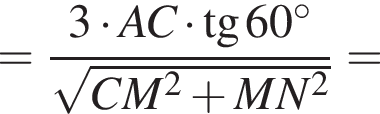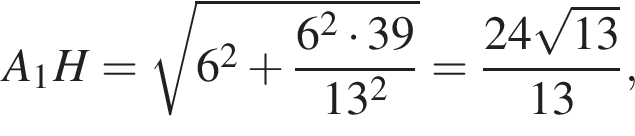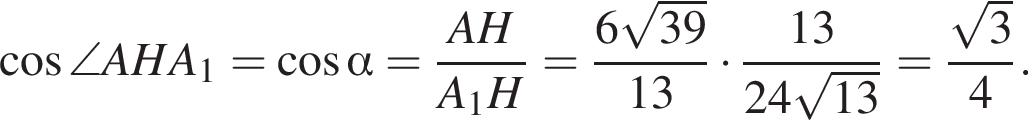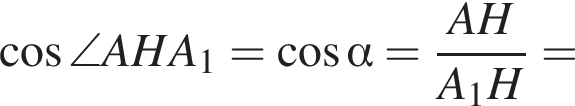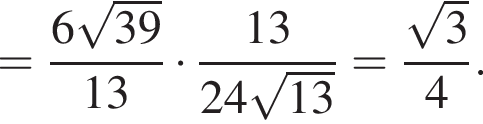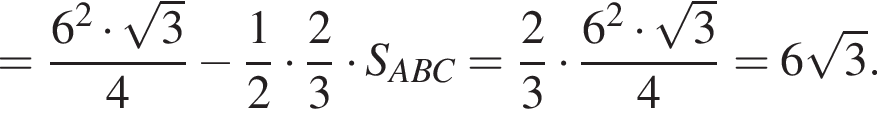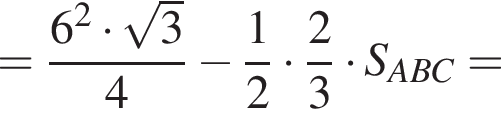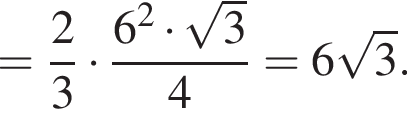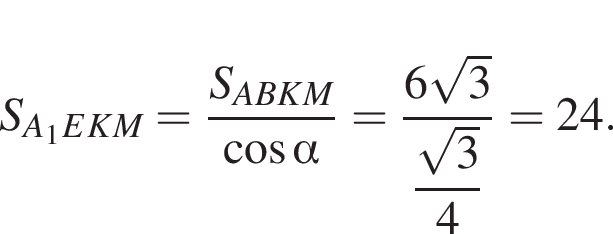Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
Значение выражения 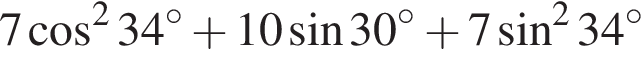 равно:
равно:
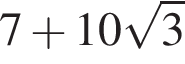
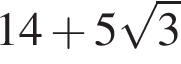
На координатной прямой отмечены точки А, В, С, D, E. Если расстояние между A и С равно ![]() то ближе других к точке с координатой 0,5 расположена точка:
то ближе других к точке с координатой 0,5 расположена точка:
Последовательность задана формулой n-го члена 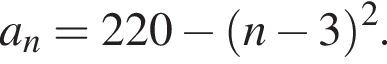 Вычислите
Вычислите 
Значение выражения 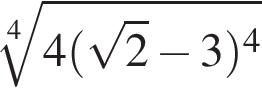 равно:
равно:
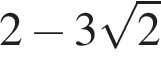
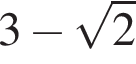
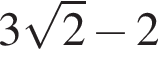
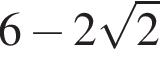
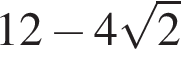
Если MK — диаметр, O — центр окружности,
 (см. рис.), то градусная мера вписанного угла NMK равна:
(см. рис.), то градусная мера вписанного угла NMK равна:
Количество целых решений неравенства 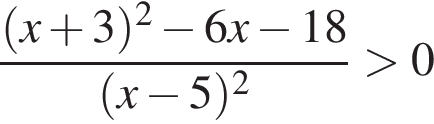 на промежутке
на промежутке 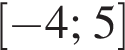 равно:
равно:
Свежие фрукты при сушке теряют a % своей массы. Укажите выражение, определяющее массу сухих фруктов (в килограммах), полученных из 20 кг свежих.
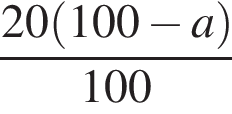
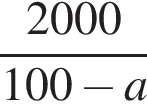
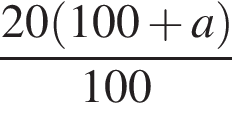
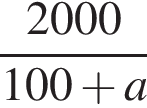
Укажите уравнение, равносильное уравнению 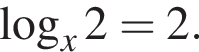
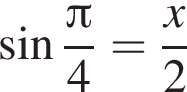
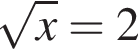
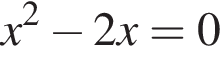
В треугольнике ABC 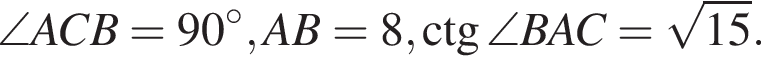 Найдите длину стороны CB.
Найдите длину стороны CB.
Найдите сумму целых решений (решение, если оно единственное) системы неравенств 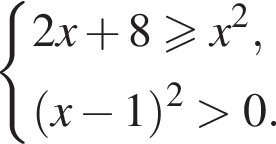
Найдите сумму корней (корень, если он единственный) уравнения 
На диаграмме показано количество посещений сайта на протяжении недели (со вторника по воскресенье). Установите соответствие между вопросами А−В и ответами 1−6.
A) В какой день недели было на 20 посещений больше, чем в предыдущий?
Б) В какой день недели количество посещений было на 35% меньше, чем во вторник?
B) В какой день недели количество посещений было на 10% больше, чем в предыдущий?
1) Вторник
2) Среда
3) Четверг
4) Пятница
5) Суббота
6) Воскресенье
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Выберите три верных утверждения:
1) если 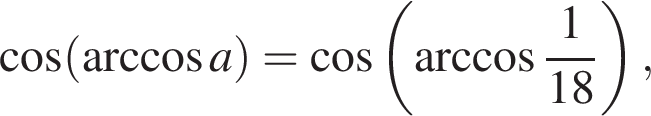 то
то 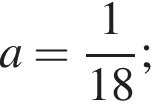
2) если 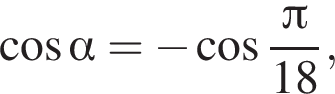 то
то 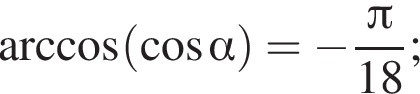
3) если 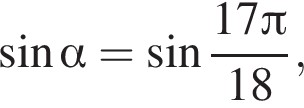 то
то 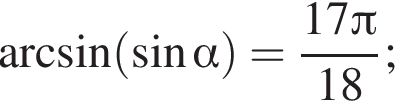
4) если 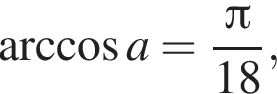 то
то 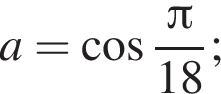
5) если 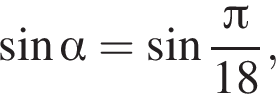 то
то 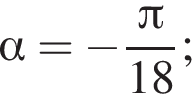
6) если 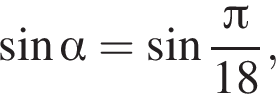 то
то 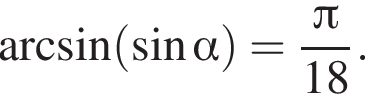
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Градусная мера угла ABC равна 126°. Внутри угла ABC проведен луч BD, который делит данный угол в отношении 1 : 6 (см. рис.). Найдите градусную меру угла 1, если BO — биссектриса угла DBC.
В основании прямой четырехугольной призмы ABCDA1B1C1D1 лежит трапеция ABCD, у которой ∠C = 90°, BC и AD — основания, BC = CC1. Плоскость, которая проходит через ребро DC и вершину A1 призмы, образует угол
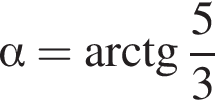 с плоскостью основания (см. рис.) и отсекает часть NC1CA1D1D. Если объем призмы равен 48, то объем оставшейся части равен … .
с плоскостью основания (см. рис.) и отсекает часть NC1CA1D1D. Если объем призмы равен 48, то объем оставшейся части равен … .
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Пусть (x1; y1), (x2; y2) — решения системы уравнений 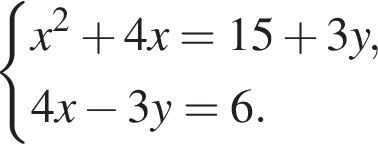
Найдите значение выражения 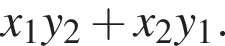
Найдите сумму всех натуральных чисел a, для которых выполняется равенство 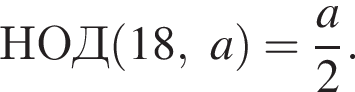
Найдите произведение наибольшего решения на количество решений уравнения 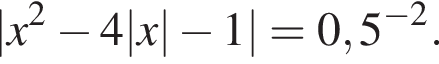
Найдите произведение наименьшего корня (в градусах) на количество различных корней уравнения  на промежутке (−90°; 90°).
на промежутке (−90°; 90°).
Найдите значение выражения 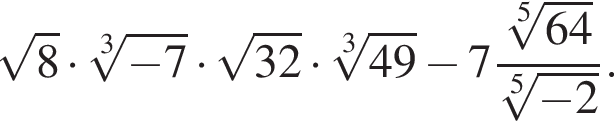
На рисунке изображен график функции 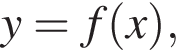 заданной на промежутке
заданной на промежутке 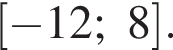 Найдите произведение значений аргумента, при которых
Найдите произведение значений аргумента, при которых 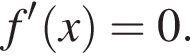 (Черными точками отмечены узлы сетки, через которые проходит график функции
(Черными точками отмечены узлы сетки, через которые проходит график функции 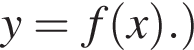
Найдите значение выражения 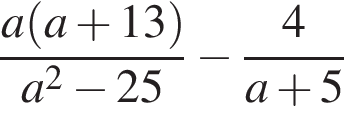 при
при 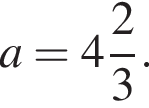
В равнобокой трапеции большее основание вдвое больше каждой из остальных сторон и лежит в плоскости α. Боковая сторона образует с плоскостью α угол, синус которого равен ![]() Найдите 36sinβ, где β — угол между диагональю трапеции и плоскостью α.
Найдите 36sinβ, где β — угол между диагональю трапеции и плоскостью α.
В прямоугольнике ABCD выбраны точки L на стороне BC и M на стороне AD так, что ALCM — ромб. Найдите площадь этого ромба, если AB = 3, BC = 9.
Найдите все пары (m, n) целых чисел, которые связаны соотношением m2 + 2m = n2 + 6n + 13. Пусть k — количество таких пар, m0 — наименьшее из значений m, тогда значение выражения k · m0 равно ... .
Найдите произведение корней уравнения 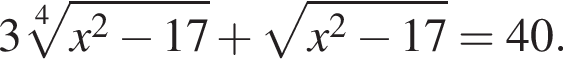
Найдите произведение наибольшего целого решения на количество всех натуральных решений неравенства 
ABCA1В1С1 — правильная треугольная призма, у которой сторона основания и боковое ребро имеют длину 6. Через середины ребер АС и BB1 и вершину A1 призмы проведена секущая плоскость. Найдите площадь сечения призмы этой плоскостью.


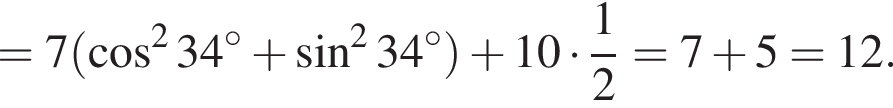
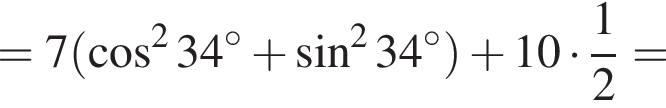
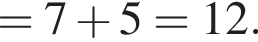
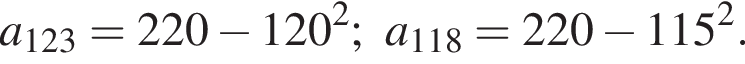 Воспользуемся формулой разности квадратов:
Воспользуемся формулой разности квадратов: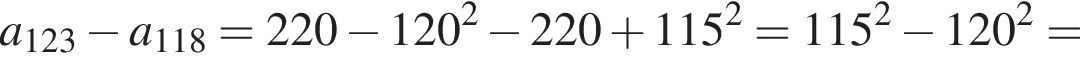
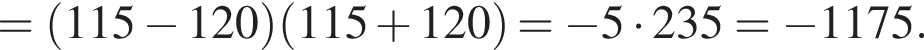
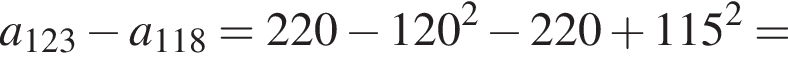
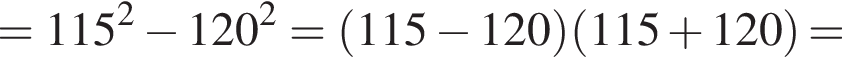
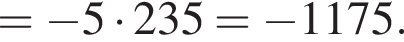
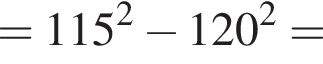
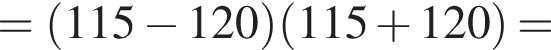
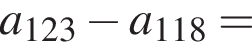
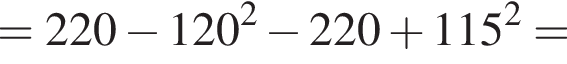
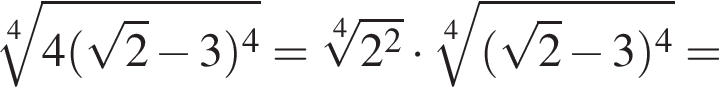
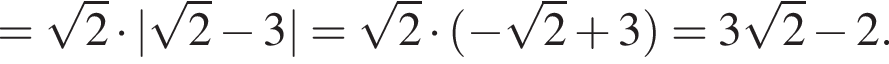

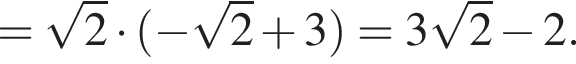
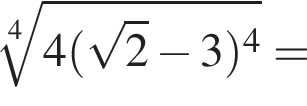
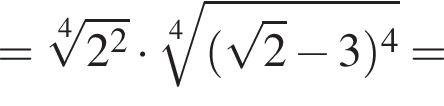
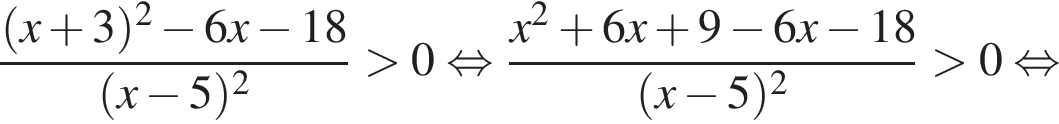
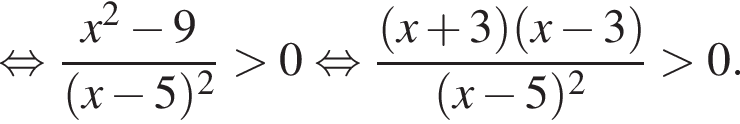
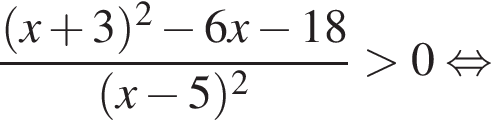
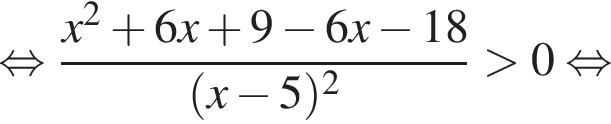
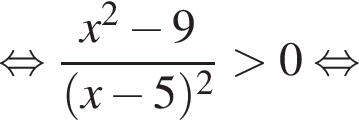
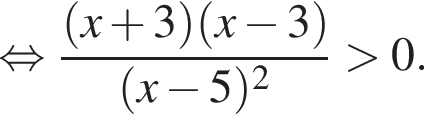
 Корни знаменателя
Корни знаменателя 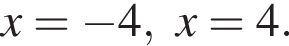 Следовательно, существует только 2 целых решения.
Следовательно, существует только 2 целых решения. 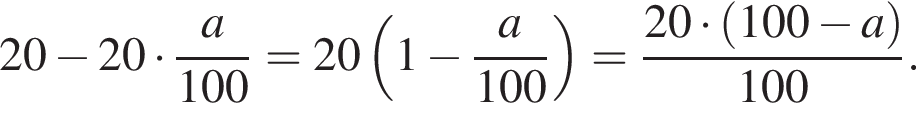
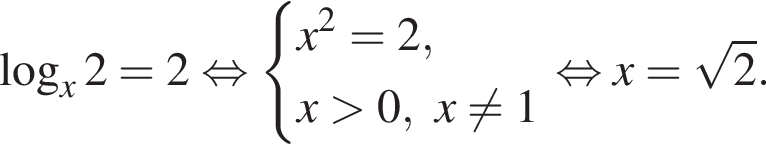
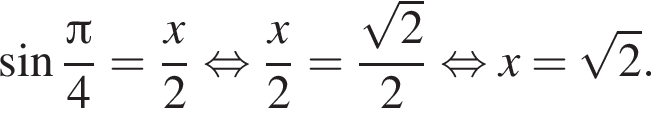
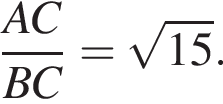 Из теоремы Пифагора:
Из теоремы Пифагора: Подставим одно выражение в другое и решим уравнение:
Подставим одно выражение в другое и решим уравнение: 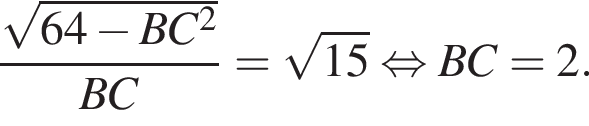
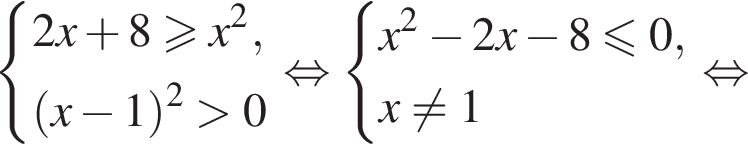
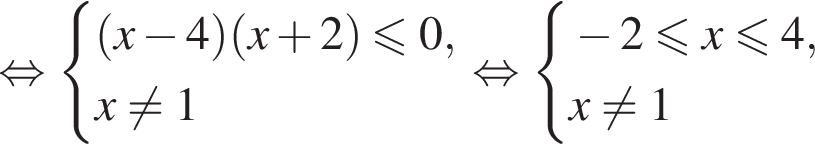
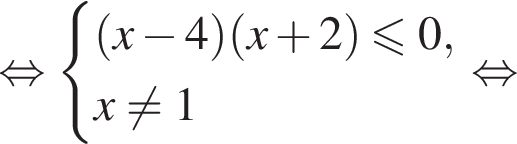
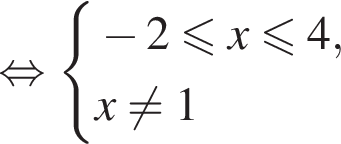
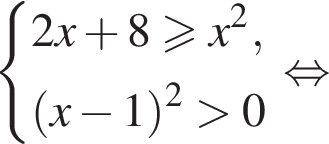
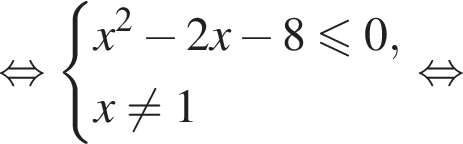
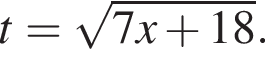 Тогда:
Тогда: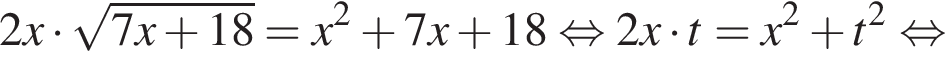

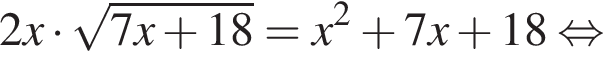


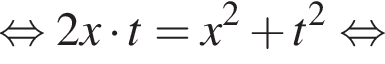
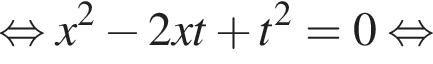
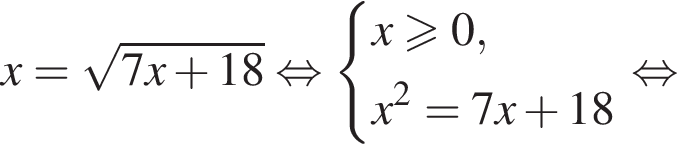
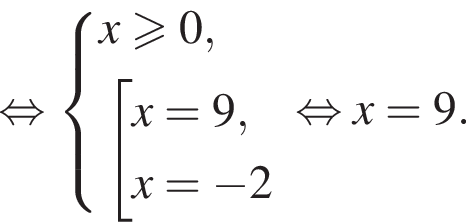
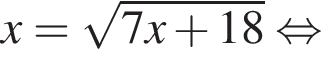
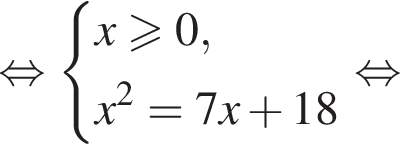
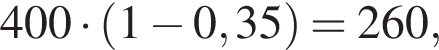 значит, количество посещений на 35% меньше, чем во вторник было в четверг (3).
значит, количество посещений на 35% меньше, чем во вторник было в четверг (3).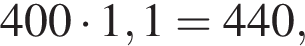 значит, в среду количество посещений было на 10% больше, чем в предыдущий (2).
значит, в среду количество посещений было на 10% больше, чем в предыдущий (2).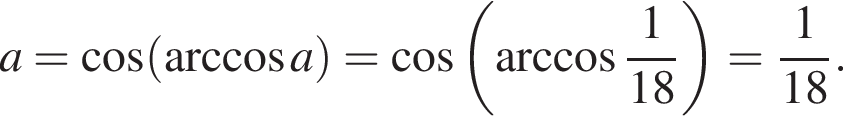

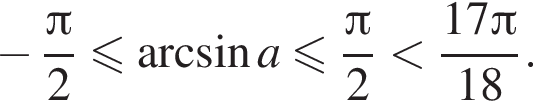
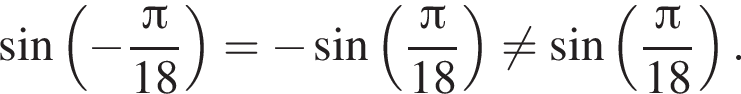
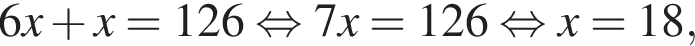
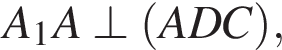
 следовательно, по теореме о трех перпендикулярах
следовательно, по теореме о трех перпендикулярах 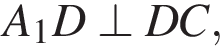 поэтому
поэтому  откуда
откуда 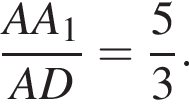 Пусть
Пусть 
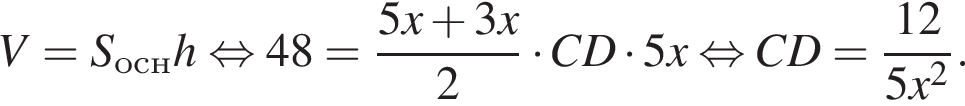
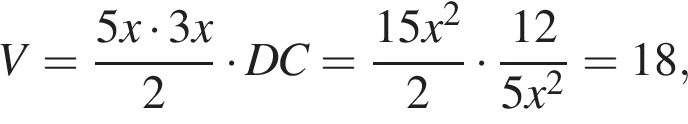 откуда
откуда 
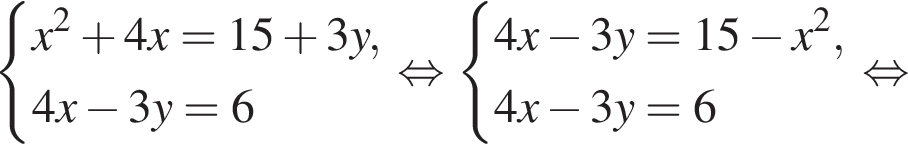
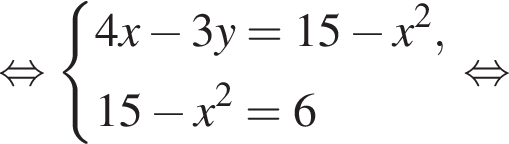
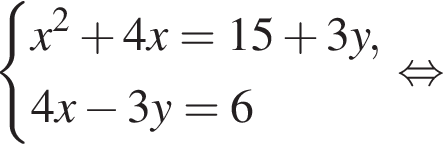
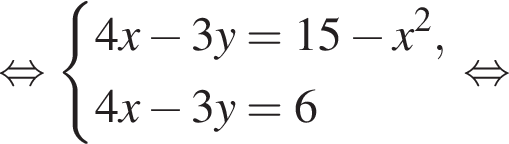
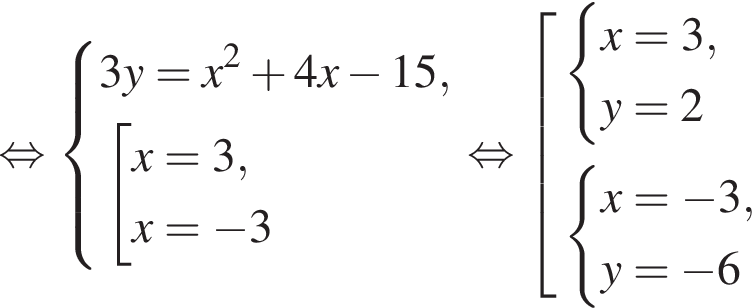


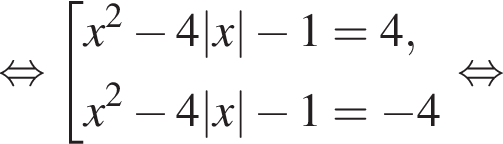
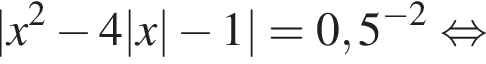
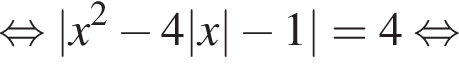
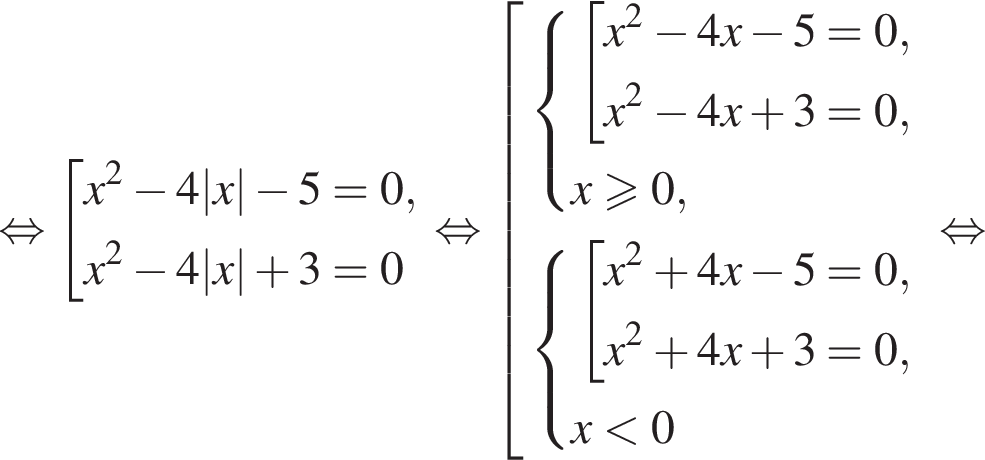
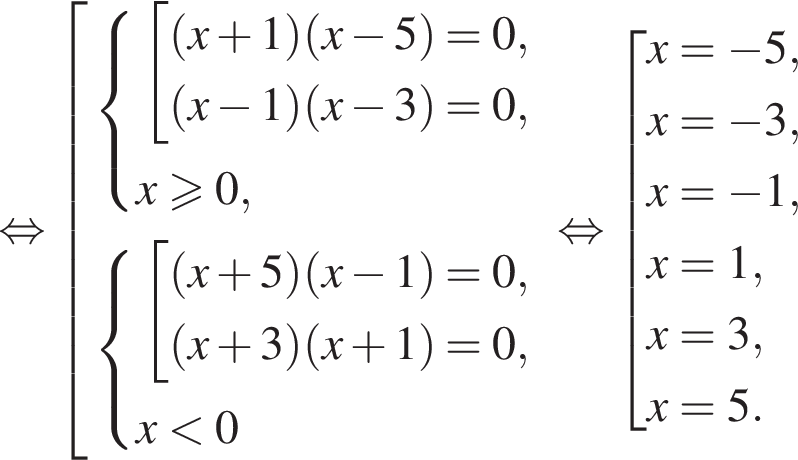
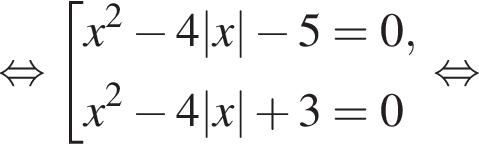
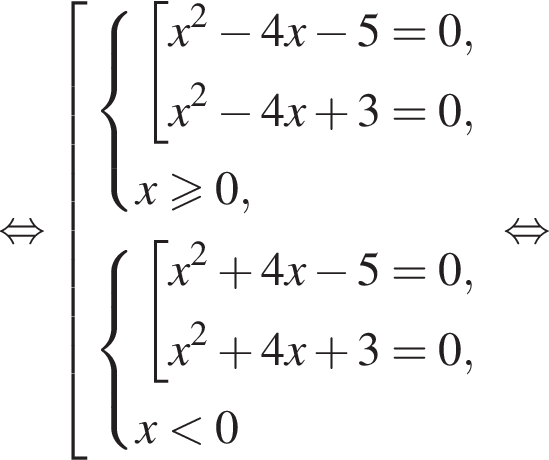
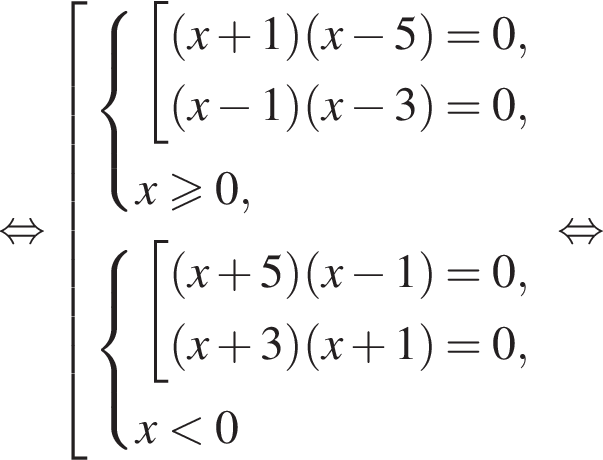
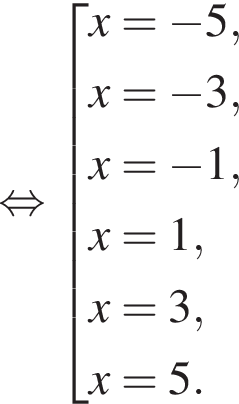
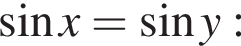
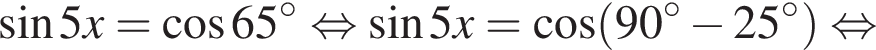
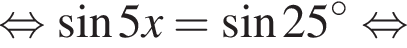
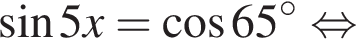

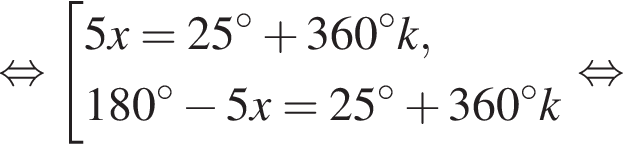
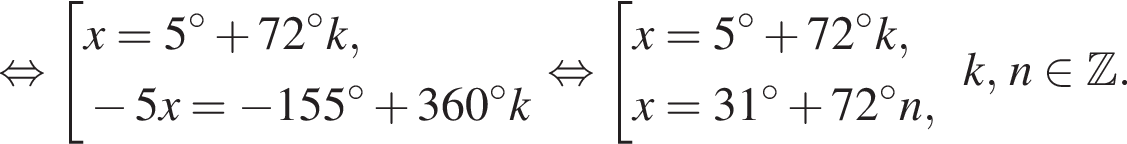
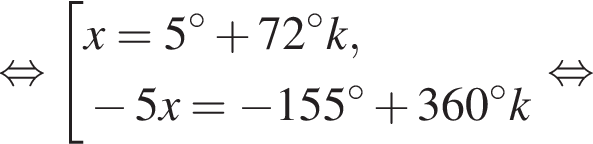
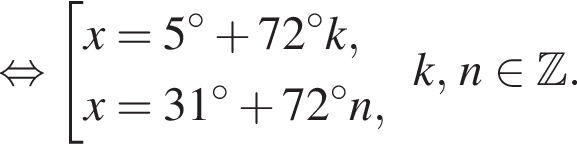

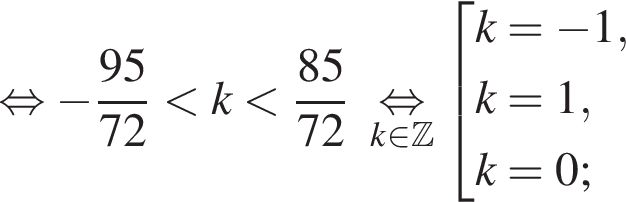


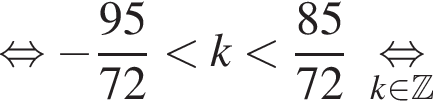
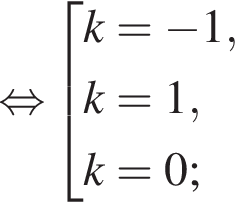

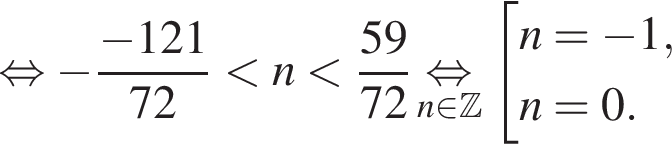
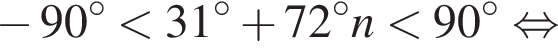

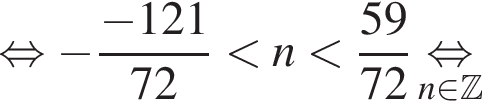
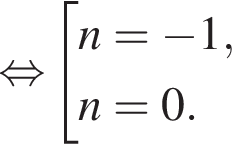
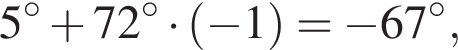
 и
и 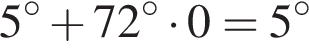 из первой серии и корни
из первой серии и корни  и
и 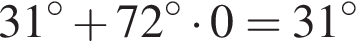 из второй. Наименьший из корней равен
из второй. Наименьший из корней равен 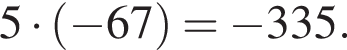
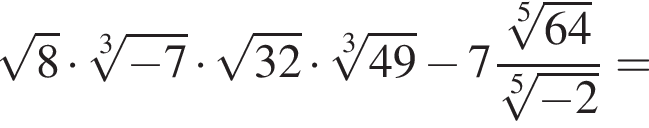
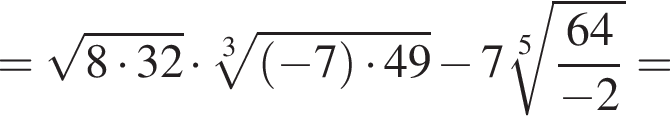
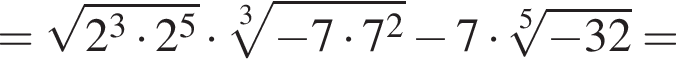
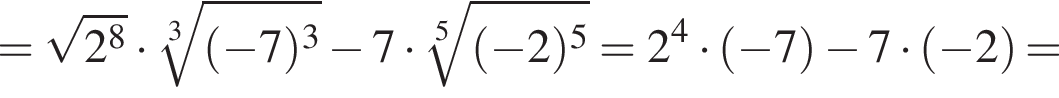
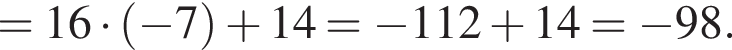
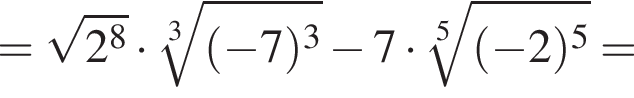
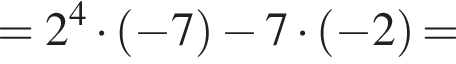
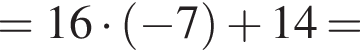

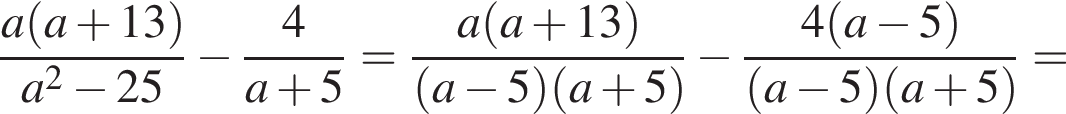
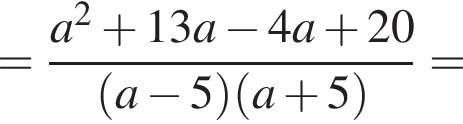
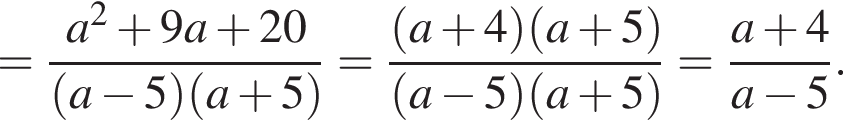
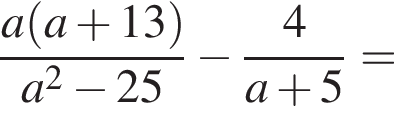
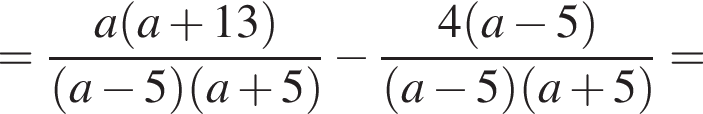
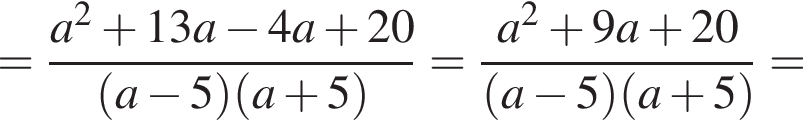
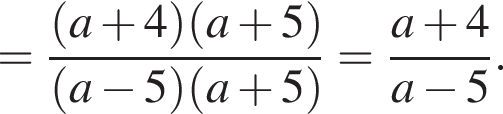
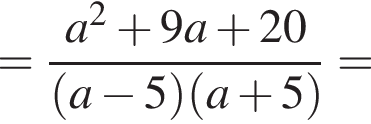
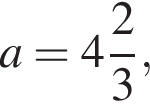 получаем:
получаем: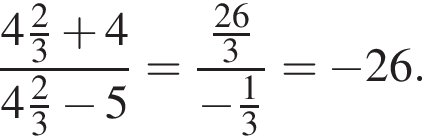
 Поскольку все стороны трапеции, кроме большего основания равны a, получим
Поскольку все стороны трапеции, кроме большего основания равны a, получим  Тогда
Тогда 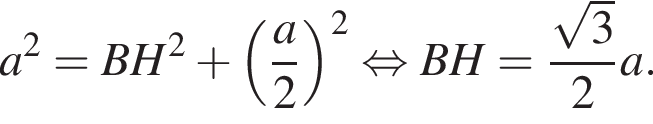

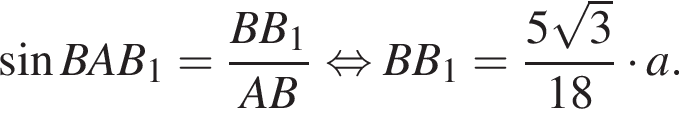
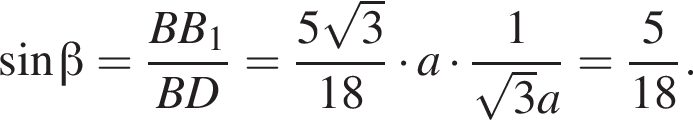
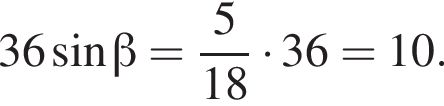
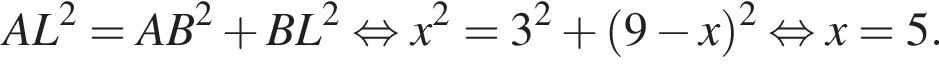
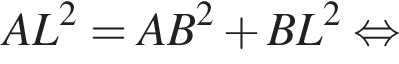
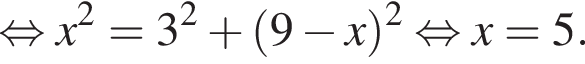
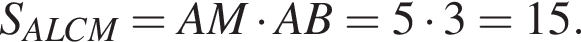
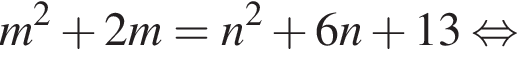
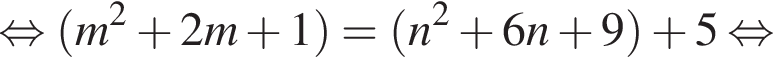
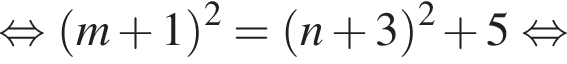

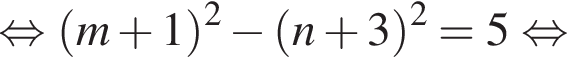

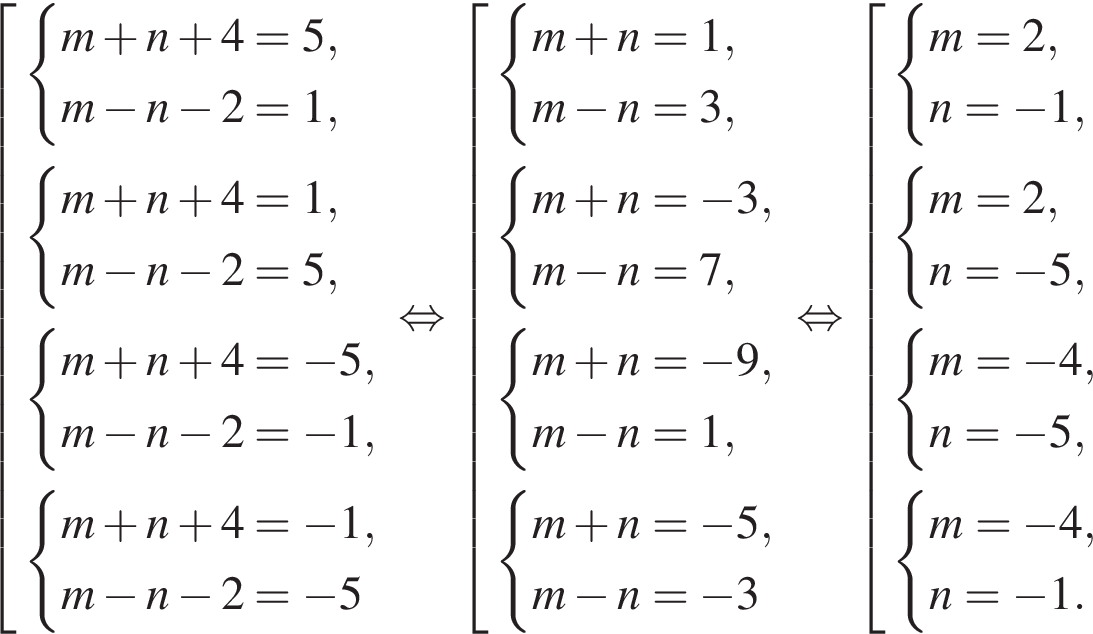
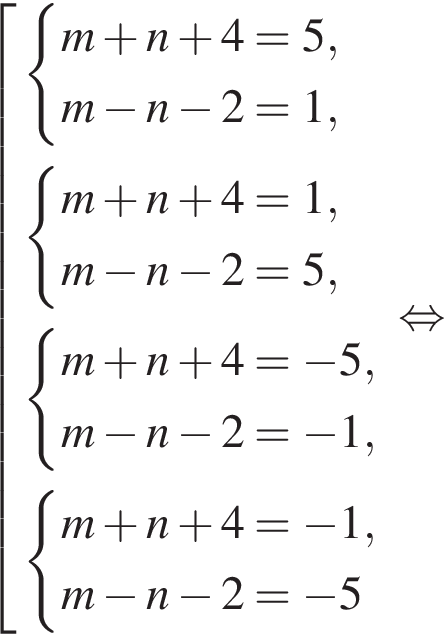
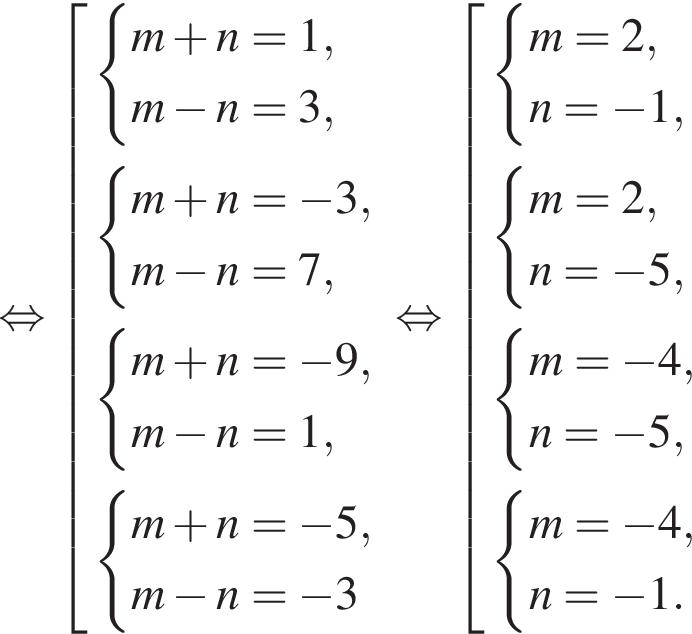
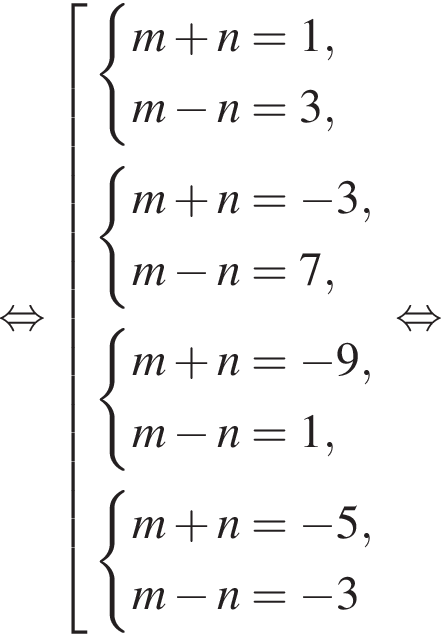
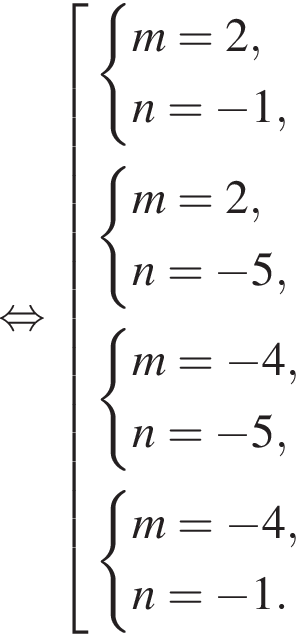
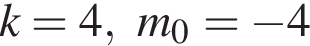 и
и 
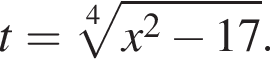 Тогда:
Тогда:
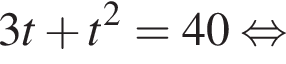
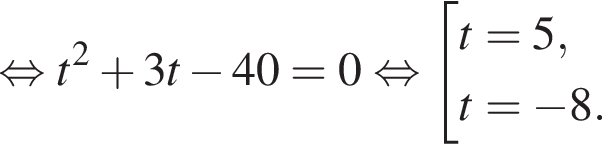
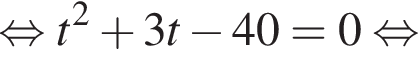
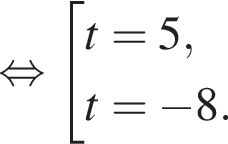
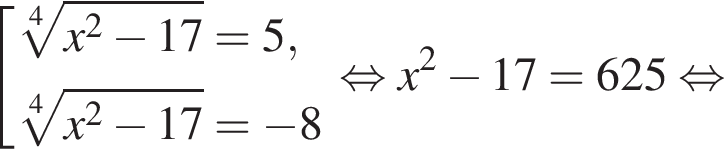
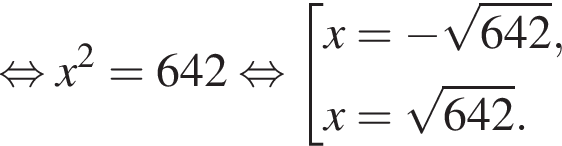
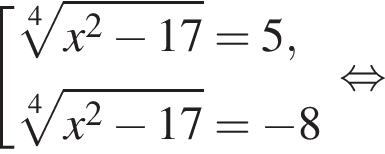
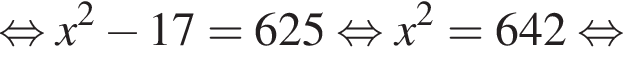
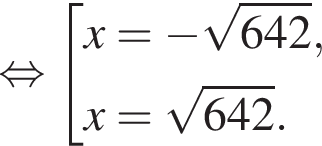
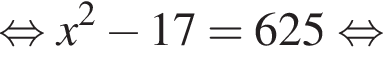

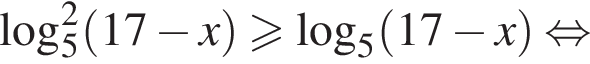
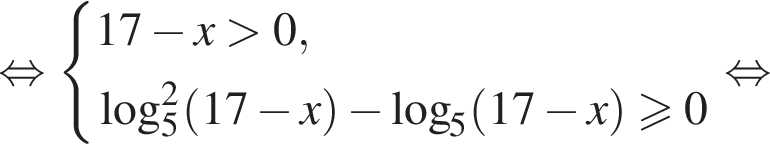
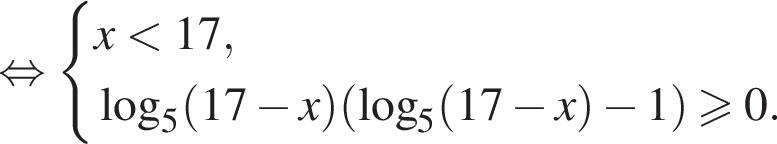
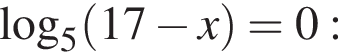
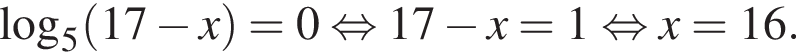
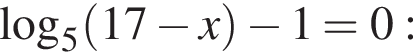

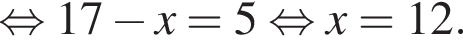
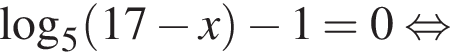
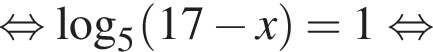
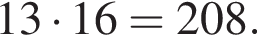
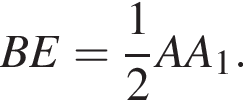 Отрезки CB и NM есть медианы треугольника ACN, поэтому CK : KB = 2 : 1, то есть CK = 4, BK = 2.
Отрезки CB и NM есть медианы треугольника ACN, поэтому CK : KB = 2 : 1, то есть CK = 4, BK = 2.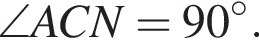 Тогда
Тогда 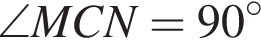 и
и